3 4 5 треугольник

Общие свойства

Образец, полученный путём раскраски только нечётных чисел, очень похож на фрактал, называемый треугольником Серпинского. Это сходство становится всё более точным, так как рассматривается больше строк в пределе, когда число рядов приближается к бесконечности, получающийся в результате шаблон представляет собой фигуру, предполагающую фиксированный периметр. В целом числа могут быть окрашены по-разному в зависимости от того, являются ли они кратными 3, 4 и т. д.

В треугольной части сетки количество кратчайших путей от заданного до верхнего угла треугольника является соответствующей записью в паскалевском треугольнике. На треугольной игровой доске Плинко это распределение должно давать вероятности выигрыша различных призов. Если строки треугольника выровнены по левому краю, диагональные полосы суммируются с числами Фибоначчи.

Благодаря простому построению факториалами можно дать очень простое представление фигуры Паскаля в терминах экспоненциальной матрицы: треугольник — это экспонента матрицы, которая имеет последовательность 1, 2, 3, 4… на её субдиагонали, а все другие точки — 0.

Шаблон, созданный элементарным клеточным автоматом с использованием правила 60, является в точности паскалевским треугольником с биномиальными коэффициентами, приведёнными по модулю 2. Правило 102 также создаёт этот шаблон, когда завершающие нули опущены. Правило 90 создаёт тот же шаблон, но с пустой ячейкой, разделяющей каждую запись в строках. Фигура может быть расширена до отрицательных номеров строк.

Небольшие хитрости

Египетский треугольник 3х4х5 актуален для маленьких домов. Но, что делать, если дом 12х15?

Для этого нужно построить прямоугольный треугольник, у которого катеты равняются 12 и 15 м. Гипотенуза находится как квадратный корень из суммы 12х12 и 15х15. В итоге получаем 19,2 м. С помощью чего-либо — веревки, шпагата, бечевки, тросика, военного кабеля, отмеряем 12, 15 и 19,2 м. Делаем узлы на этих местах и ставим жимки.

Затем треугольник нужно растянуть на нужном месте и установить 3 точки опоры, в которые вбить колышки. Четвертую точку можно получить, не трогая концы катетов. Для этого точка прямого угла перекидывается по диагонали и все готово.

Например, есть участок, где требуется прямой угол – для места под кухонный гарнитур, раскладки кафеля и других моментов. Хорошо бы такие вопросы учесть при кладке, но реальность другая и не всегда попадаются ровные стены и прямые углы. Здесь пригодится египетский треугольник с соотношением 3:4:5, либо при необходимости 1,5:2:2,5.

Обязательно учитывается толщина маяков, погрешность, бугры на стенах и т.д. Треугольник рисуется с помощью рулетки и мела. Если разметка небольшая, то можно воспользоваться листом гипсокартона, так как режутся они с правильными углами.

Египетский треугольник широко использовался в строительстве целых 2,5 века. И сегодня иногда приходится применять данную методику, при отсутствии необходимых инструментов, чтобы получить прямые углы. Свойства этой фигуры уникальны, что гарантирует точность в архитектуре и строительстве, без которой не обойтись. С ним легко работать, по форме он гармоничен и красив. До сих пор пытливые умы пытаются разгадать тайну египетского треугольника.

История открытия

Название египетский треугольник получил благодаря эллинам и Пифагору, которые были частыми гостями в Египте. И случилось это приблизительно в VII-V веках до н. э.

Знаменитая пирамида Хеопса, вообще-то представляет собой прямоугольный многоугольник, а вот священным египетским треугольником принято считать пирамиду
Хефрена.

Жители Египта природу Египетского треугольника, как писал Плутарх, сопоставляли с семейным очагом. В их трактовках можно было услышать, что в этой геометрической фигуре ее вертикальный катет символизировал мужчину, основание фигуры относилось к женскому началу, а гипотенузе пирамиды отводилась роль ребенка.

А уже из изученной темы вам хорошо известно, что соотношение сторон этой фигуры равно 3:4:5 и, следовательно, что это нас приводит к теореме Пифагора, так как 32 + 42= 52.

И если учесть, что в основании пирамиды Хефрена лежит египетский треугольник, то можно сделать вывод, народ древнего мира знал знаменитую теорему еще задолго до того, как она была сформулирована Пифагором.

Основной особенностью египетского треугольника, скорее всего, было его своеобразное соотношение сторон, которое было первым и простейшим из Героновых треугольников, так как и стороны, и его площадь имели целые числа.

Описанная окружность треугольника

Окружность, проходящая по всем вершинам треугольника, называется описанной окружностью. Любой треугольник может быть описан единственной окружностью.

Центр описанной окружности — это точка пересечения перпендикуляров оснований, проходящих через середину основания.

На рисунке хорошо видно, как из середины оснований мы провели перпендикуляры и нашли точку пересечения. С помощью штангенциркуля выставляем радиус от центра до любой вершины и круговым движением рисуем описанную окружность.

У прямоугольного треугольника центр описанной окружности лежит на середине гипотенузы.

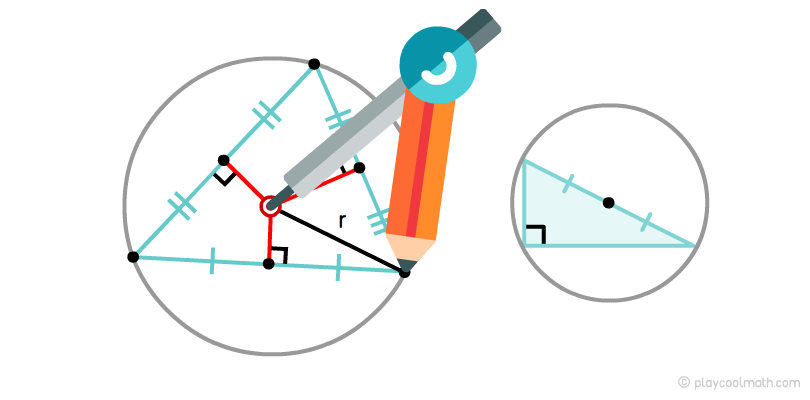
Найди на рисунке треугольник, который одновременно прямоугольный и равнобедренный.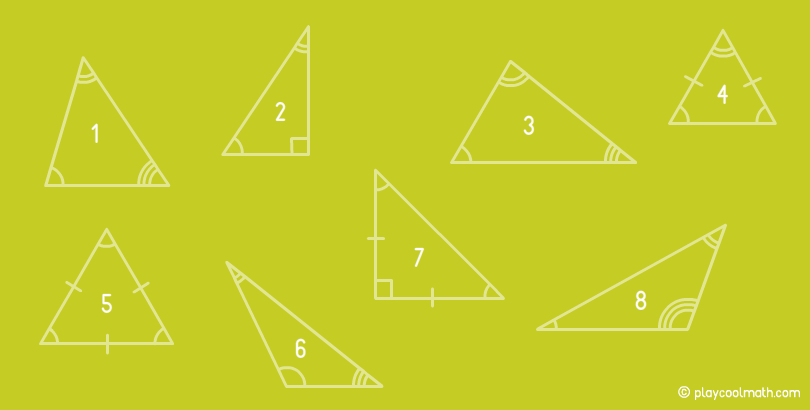

Египетский треугольник в строительстве. Общие сведения

Зарождение идеи

Идея у математика появилась после путешествия в Африку по просьбе Фалеса, который поставил задачу Пифагору изучить математику и астрономию тех мест. В Египте он среди бескрайней пустыни встретил величественные строения, поразившие его размером, изяществом и красотой.

Надо заметить, что более двух с половиной тысяч лет назад пирамиды были несколько другими – огромными, с четкими гранями. Тщательно изучив могущественные постройки, коих было не мало, так как рядом с великанами, стояли храмы поменьше, построенные для детей, жен и других родственных лиц фараона, это натолкнуло его на мысль.

Благодаря своим математическим способностям, Пифагор сумел определить закономерность в формах пирамиды, а умение анализировать и делать выводы привели к созданию одной из самых значимых теорий в истории геометрии.

Из истории

Знали ли в древнем Египте о геометрии и математике? Конечно да. Жизнь египтян была тесно связана с наукой. Они регулярно пользовались знаниями при разметке полей, создании архитектурных шедевров. Даже существовала своя служба землемеров, которые применяли геометрические правила, занимаясь восстановлением границ.

Название треугольник получил благодаря эллинам, которые нередко бывали в Египте в VII-V вв. до н.э. Считается, что прообразом фигуры стала пирамида Хеопса, отличающаяся совершенными пропорциями. Ее место особенное в истории. Если посмотреть поперечное сечение, то можно отметить два треугольника, у которых угол внутри равняется 51о50’.

Строение

Сегодня это строение усеченной формы, приобретенной под воздействием времени, высота явно потерялась. Однако, восстановив ее геометричность, можно сделать вывод, что стороны треугольников равны. Получается в основе заложен золотой прямоугольный треугольник.

Однако, следует рассмотреть другую пирамиду – Хефрена, у которой основа как раз-таки прямоугольный треугольник и где угол наклона боковых граней равен 53о12 с соотношением катетов 4:3. Это уже так называемый священный треугольник. Для египтян такая фигура сопоставлялась с семейным очагом: катет вертикального положения олицетворял мужчину, основание – представительницу прекрасного пола, а гипотенуза – рождение ребенка от обоих.

Стороны пирамиды Хефрена в соотношении равны 3:4:5, что точно соответствует теореме Пифагора. Значит, можно сделать вывод, что строители уже знали об этой теореме, но не могли ее сформулировать. Хотя, в исторических письменах встречаются следы использования египетского треугольника за много веков даже до Египта. До сегодняшнего дня это загадка, как могли такие знания получить древние египтяне. Понимали ли они чем обладают?

Особенность фигуры к тому же в том, что благодаря подобному соотношению, она является простым и первым Героновым треугольником, так как ее стороны и площадь целочисленные.

Обратное доказательство

Как доказать, что треугольник прямоугольный? Нужно порой исходить от обратного, то есть если сумма квадратов обеих сторон равна квадрату третьей, то треугольник прямоугольный, что подтверждает равенство 32х42=52 и значит он действительно прямоугольный.

Таким образом теорема Пифагора стала каноном и фундаментом развития математической науки. Со школьной скамьи каждый ученик знает, что означает выражение «Пифагоровы штаны во все стороны равны».

Интересно, что теорема Пифагора находится в Книге Гиннесса как теорема, обладающая самым большим количеством доказательств, которых примерно 500.

Особенности

Если рассмотреть более детально отличительные особенности египетского треугольника, то можно выделить следующие моменты:

• все стороны и площадь состоят из целых чисел, как говорилось выше;
• согласно теории великого математика, сумма квадратов катетов равна квадрату гипотенузе;
• такой фигурой возможно отмерить прямые углы в пространстве. Это используется в процессе строительства до сих пор;
• не обязательно пользоваться специальными измерительными приборами, подойдут подручные средства, например, веревка.

Египетский треугольник

Египетский треугольник – прямоугольный треугольник с соотношением сторон 3:4:5. Сумма указанных чисел (3+4+5=12) с древних времен использовалась как единица кратности при построении прямых углов с помощью веревки, размеченной узлами на 3/12 и 7/12 ее длины. Применялся египетский треугольник в архитектуре средних веков для построения схем пропорциональности.

Итак, с чего же начать? Разве вот с этого: 3 + 5 = 8. а число 4 составляет половину числа 8. Стоп! Числа 3, 5, 8… Разве они не напоминают что-то очень знакомое? Ну конечно, они имеют прямое отношение к золотому сечению и входят в так называемый «золотой ряд»: 1, 1, 2, 3, 5, 8, 13, 21… В этом ряду каждый последующий член равен сумме двух предыдущих: 1 + 1= 2. 1 + 2 = 3, 2 + 3 = 5, 3 + 5 = 8 и так далее. Выходит, что египетский треугольник имеет отношение к золотому сечению? И древние египтяне знали, с чем имели дело? Но не будем торопиться с выводами. Необходимо выяснить детали поточнее.

Выражение «золотое сечение», как считают некоторые, впервые ввел в XV веке Леонардо да Винчи. Но сам «золотой ряд» стал известен в 1202 году, когда его впервые опубликовал в своей «Книге о счете» итальянский математик Леонардо Пизанский. Прозванный Фибоначчи. Однако почти за две тысячи лет до них золотое сечение было известно Пифагору и его ученикам. Правда, называлось оно по-другому, как «деление в среднем и крайнем отношении». А вот египетский треугольник с его «золотым сечением» был известен еще в те далекие времена, когда строились пирамиды в Египте, когда процветала Атлантида.

Для доказательства теоремы о египетском треугольнике необходимо использовать отрезок прямой известной длины А-А1 (рис.). Он будет служить масштабом, единицей измерения, и позволит определить длину всех сторон треугольника. Три отрезка А-А1 равны по длине наименьшей из сторон треугольника ВС, у которой соотношение равно 3. А четыре отрезка А-А1 равны по длине второй стороне, у которой соотношение выражается числом 4. И, наконец, длина третьей стороны равна пяти отрезкам А-А1. А дальше, как говорится, дело техники. На бумаге проведем отрезок ВС, являющийся наименьшей стороной треугольника. Затем из точки В радиусом, равным отрезку с соотношением 5, проводим циркулем дугу окружности, а из точки С —дугу окружности радиусом, равным длине отрезка с соотношением 4. Если теперь точку пересечения дуг соединить линиями с точками В и С, то получим прямоугольный треугольнике соотношением сторон 3 : 4 : 5.

Что и требовалось доказать.

Кто строил пирамиды?

Также некоторые люди уверены, что строительством египетских пирамид занимались рабы. Но этот миф мы уже развеяли на нашем — в работу были вовлечены обычные египтяне. Строительство активно велось в периоды, когда людям не нужно было следить за сельским хозяйством. Важные задачи вроде проектирования сооружений и слежения за складыванием блоков давались архитекторам. Большинство рабочих трудились на каменоломнях — самой сложной с физической точки зрения задачей было перетаскивание блоков. По мнению ученых, в строительство каждой пирамиды было вовлечено около 20–30 тысяч египтян. Противников этого дела, судя по всему, было мало, потому что работа велась во имя фараона.

Строительство пирамиды в представлении художника

Логично предполагать, что всем рабочим нужно было где-то спать и что-то есть. Все это было доступно в специальных поселках для строителей. Останки одного из них были найдены возле трех пирамид в Гизе — египетского города на западном берегу реки Нил. Раскопки на этой территории ведутся с 1960-х годов. За все это время археологам удалось найти места захоронений архитекторов, прорабов и обычных рабочих. Их могилы сильно отличались — архитекторы, которые вносили большой вклад в проектирование пирамид, хоронились внутри гробниц. Обычные рабочие, в свою очередь, хоронились в обыкновенных могилах.

На территории поселков для строителей располагались мастерские, на которых изготовлялись инструменты. Также там были организованы места для готовки пищи для рабочих: хлебопекарные цеха, пивоварни и кладовые для сушки рыбы. Вдобавок ко всему этому, археологами были найдены места для принесения жертв покойным фараонам. Судя по всему, Древний Египет был богатым местом, потому что жители могли себе позволить приношение даже молодых животных.

Пиво считается основным алкогольным напитком Древнего Египта

Классификация треугольников по сторонам

Равносторонний треугольник

Равносторонний треугольник или правильный треугольник — это треугольник, у которого все стороны равны. У равностороннего треугольника все углы равны 60°.

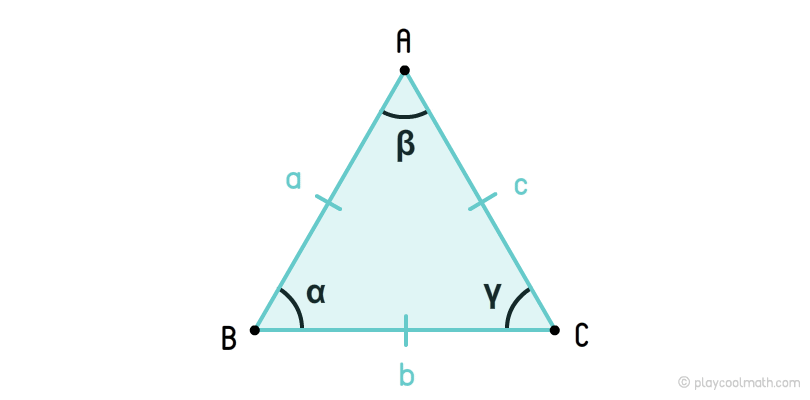
На рисунке мы обозначили стороны как a, b, c, где a = b = c. Углы обозначили как α, β, γ, где α = β = γ = 60°. Одинаковые стороны помечаются одинаковым количеством черточек. Мы пометили стороны a, b, c одной чертой. Одинаковые углы помечаются одинаковым количеством дуг. На рисунке мы все углы пометили одной дугой.

Неравносторонний треугольник

Неравносторонний треугольник — это треугольник, у которого все стороны не равны. У неравностороннего треугольника углы тоже не равны.

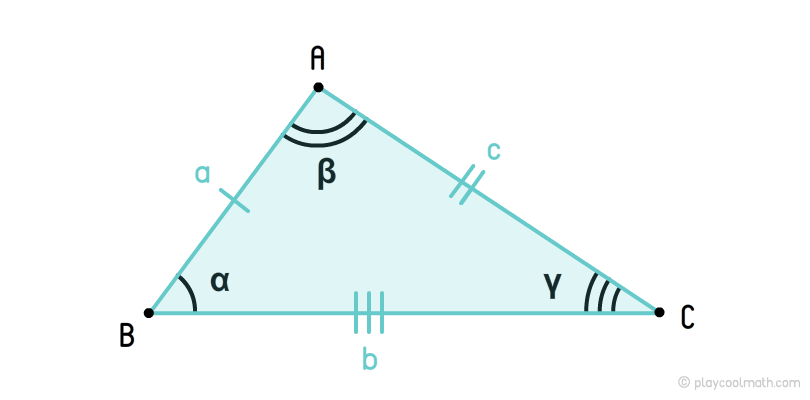
На рисунке мы обозначили стороны a, b, c, где a ≠ b ≠ c. Углы обозначили как α, β, γ, где α ≠ β ≠ γ. Мы пометили стороны a, b, c разным количеством черточек, указав что все стороны имеют разную длину. Все углы пометили разным количеством дуг, указав, что все углы имеют разные угловые меры.

Равнобедренный треугольник

Равнобедренный треугольник — это треугольник, у которого две стороны равны. Эти стороны называются боковыми или бедрами, а третья сторона называется основанием.

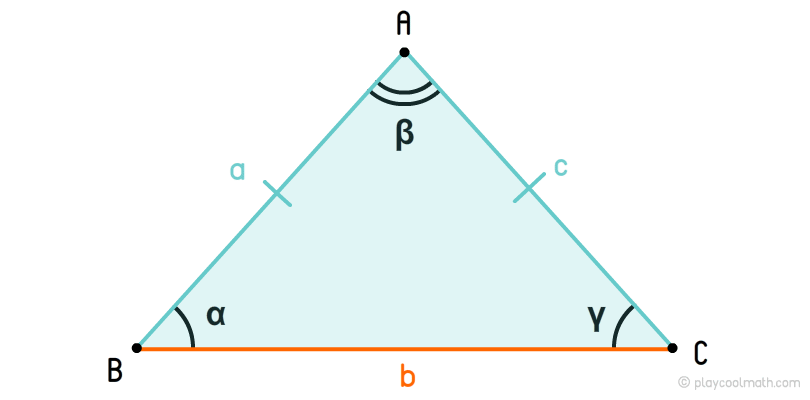
На рисунке мы обозначили боковые стороны как a, c, где a = c, а основание b, где b ≠ a и b ≠ c. У равнобедренного треугольника углы у основания равны α = γ.

История египетского треугольника

Создателем этой геометрической конструкции является один из величайших математиков древности Пифагор. Именно благодаря его математическим изысканиям мы можем в полной мере использовать все свойства данного геометрического построения в строительстве.

Отношение самой длинной стороны этого треугольника к самой короткой стороне – «два к одному». То есть самая длинная сторона в два раза длиннее самой короткой стороны. Она также изготовлена ​​из пластика и широко используется в дизайне, рисовании и Строительных приложений.

Вы можете найти бесконечное количество примеров правильных треугольников. Один из самых известных – «Треугольник 3, 4, 5». Египтяне использовали этот треугольник для съемки земли. Некоторые считают, что они также использовали его для разработки своих пирамид. Плотники и деревообработчики также используют его, чтобы сделать их углы квадратными. Он доказал, что для правого треугольника сумма квадратов двух сторон, которые соединяются под прямым углом, равна квадрату третьей стороны. Третья сторона – сторона, противоположная правому углу, называется гипотенузой правого треугольника.

Можно предположить, что математические навыки позволили Пифагору заметить закономерность в формах строения. Дальнейшее развитие событий можно легко представить. Базовый анализ и построение выводов создали одну из самых значимых фигур в истории. Скорее всего, в качестве прообраза была выбрана именно пирамида Хеопса из-за своих практически совершенных пропорций.

Две более короткие стороны обычно называются «ногами». Эта формула называется Пифагорейской теоремой в честь Пифагора. Мы можем проверить, что теорема Пифагора верна, подставляя значения. Квадратный корень из 169 равен 13, которая является мерой гипотенузы в этом треугольнике. Теорема Пифагора имеет много применений. Вы можете использовать его, чтобы проверить, является ли треугольник правильным треугольником. Или вы можете использовать его, чтобы найти недостающие меры сторон.

Подставьте значения в формулу и выполните вычисления, как это. Джимми Данн пишет как Алан Уинстон. До того, как произошла физическая ориентация и расположение новой пирамиды, необходимо было провести значительное планирование под руководством «королевского мастера-строителя». В конечном итоге ответственность возлагалась на визиря, который, как правило, возглавлял все королевские работы. Первым шагом в этом процессе стали специалисты, которые разработали планы пирамиды на папирусе. После начала строительства планы и эскизы были сделаны на папирусах или плоских плитах из известняка.

Как добраться?

Быстрее всего добраться к Египетскому мосту в Санкт-Петербурге можно от станции метро «Балтийская». Нужно выйти на этой станции и проследовать на Обводный канал. Оттуда свернуть на Лермонтовский проспект, по которому нужно пройти еще минут 10-15. Вдали появятся очертания известных зеленых обелисков под светом фонарей, и там же – фигуры сфинксов, охраняющих вход на мост.

Если есть немного свободного времени и желания пройтись, также можно выйти на станции «Технологический Институт», оттуда перейти на 1-ю Красноармейскую, а затем свернуть на проспект Троицкий. Так можно будет по дороге посмотреть Троицкий собор Санкт-Петербурга.

Адрес: г. Санкт-Петербург, Набережная реки Фонтанки, 151-153.

Watch this video on YouTube

Иные способы выведения прямого угла

Если нет желания заниматься выведением углов самостоятельно, а финансы позволяют обратиться за помощью к специалистам, можно вообще не думать об этом вопросе. Один звонок − и на участке уже находится геодезист с теоделитом, который в сжатые сроки сделает разметку. Однако в этом случае необходимо быть готовым к внушительным затратам на оплату его труда.

ФОТО: omegagalvanoplastia.com.brТеоделит – высокоточная техника, однако стоимость подобной разметки может влететь «в копеечку»

Если говорить о минимальных затратах, то, основываясь на прайс-листах фирм, оказывающих подобные услуги, вызов и работа геодезиста с инструментом обойдётся в 1 000 руб./час при минимальной оплате 7 000 руб. Дальше − больше. Разметка осей (2 точки) – ещё 3 000 рублей. Если же потребуется определить точные координаты по GPS, то здесь каждые три точки обойдутся владельцу в 5 000 руб. Можно посчитать, какова будет общая сумма (все цены указаны с учётом на конец сентября 2020 года). Не проще ли самому произвести все необходимые разметки? Ведь сэкономленные средства всегда можно потратить на что-то полезное в дальнейшем строительстве.

ФОТО: thelundreport.orgСтоит приготовиться к тому, что карман значительно облегчится

Конструкция

Новая переправа не была создана по подобию старого. Основной целью нового Египетского моста в Питере было соединить два берега реки Фонтанки, при этом оставаясь легкой и не затратной конструкцией. Но совсем отойти от применения мотивов Древнего Египта новые архитекторы не решились.

В дизайне использовались украшения лавровыми венками и цветами лотоса. Также сохранились сфинксы, что и позволило оставить прежнее название.

Последнюю реконструкцию чугунных сфинксов провели в 2004 году, обнаружив первоначальный слой позолоты на их головах. Скульптуры были сильно повреждены, во многих местах имелись трещины. Все отпечатки времени удалили, скульптуры снова позолотили. На сегодня сфинксы относятся к старейшим памяткам культуры Санкт-Петербурга.

Примечания и ссылки

1. ^ «Египетский треугольник» также используется Виолле-ле-Дюк для обозначения треугольника с основанием 8 и высотой 5, который он считает направляющим элементом вертикальной планировки нескольких готических соборов , один из которых — Нотр-Дам де Пари . В «Трактате об Исиде и ОсирисеПлутарха упоминается его использование египтянами, которые заимствовали его из египетского священного треугольника (3, 4, 5).
2. ↑ После пяти тысяч лет использования и изучения информация настолько разрознена, что практически невозможно дать полный список того, где находится каждое утверждение (все опубликовано, и здесь нет ничего оригинального).
3. ^ Под «примитивной тройкой» понимается, что ее элементы не имеют общих делителей, кроме единицы; то есть они являются простыми числами друг для друга два на два.
4. ↑ Термин «Диофантова» или «Диофантова» была создана в честь Диофанта из Александрии и обозначает задачи , в которых интересно найти целые решения. В случае прямоугольного треугольника «диофантовость» означает, что его стороны имеют целые значения произвольной единицы измерения.
5. ↑ Это глубокая и историческая причина, по которой число 1 не считается простым. Некоторые люди спрашивают, почему единица не является простым числом, если элементарное определение простого числа таково: «это число, которое имеет только единицу и само себя в качестве делителей». Нет никаких логических оснований возражать против того, что единица соответствует этому определению; настоящий мотив исходит из этих древних верований.
6. ↑ Это блок красного гранита, который не проходит через дверь, поэтому он был помещен до завершения ограждения, в котором он находится. Его внутренний объем составляет половину объема, определяемого его внешними краями (стр. 226 вышеупомянутой книги Матилы Гика).
7. ^ Они были изучены Ф. Дж. Диком и опубликованы в статье в American Mathematical Monthly .
8. ↑ Этот аспект может быть подтвержден на странице 213 и расширен на 226 аргентинском издании книги Матилы Гика, цитируемой в библиографии.

Гика, Матила (1933). Эстетика пропорций в природе и искусстве . Париж: Галлимар.  

Библиография

• Гика , Матила (1953). Эстетика пропорций в природе и в искусстве . Буэнос-Айрес, Аргентина: от редакции Посейдон.
• Данциг , Тобиас (1971). Номер. Язык науки . Буэнос-Айрес, Аргентина: редакция Hobbs Sudamericana SA. Перевод четвертого издания на английский язык, сделанный доктором Мануэлем Баланзатом и Фернандо Лидой Гарсия, исправленный и расширенный. Первое издание в Аргентине: 1947. Перевод доктора Мануэля Баланзата. Отредактировано ES Cabrera и HJ Médici и опубликовано Librería del Colegio SA
• Данциг, Тобиас (1930, 1933, 1939, 1954). Number The Languaje of Science (Критический обзор, написанный для образованных нематематиков) . Нуэва-Йорк: Компания Macmillan (оригинальная).
• Данциг, Тобиас (1967). Число. The Languaje of Science (Критический обзор, написанный для образованных нематематиков) . Нуэва-Йорк: Свободная пресса.
• Гельфонд, АО (1979). Решение уравнений в целых числах . М .: Эдиториал Мир, Сборник популярных уроков математики, глава 3, стр. 20-25. Перевод с русского инженера Кристобаля Гарсиа Галана.
• Бельский / Калужнин (1980). Неточное деление . М .: Едиториал Мир, Сборник «Популярные уроки математики», глава 4, стр. 22–26.

Этот удивительный египетский треугольник

Каждый, кто внимательно слушал в школе учителя геометрии, очень хорошо знает, что такое египетский треугольник. Из других типов похожих геометрических фигур под углом 90 градусов он имеет особые пропорции. Когда человек впервые слышит фразу «египетский треугольник», на ум приходят картины величественных пирамид и фараонов. А что говорит история?

Как это всегда бывает, в отношении названия «египетский треугольник» есть несколько теорий.По одной из них, знаменитая теорема Пифагора увидела свет именно благодаря этой фигуре. В 535 г. до н. Пифагор, следуя совету Фалеса, отправился в Египет, чтобы заполнить определенные пробелы в знаниях математики и астрономии

Там он обратил внимание на особенности работы египетских геодезистов. Они выполнили очень необычный способ построения треугольной фигуры с прямым углом, стороны которого были связаны между собой с соотношением 3-4-5

Этот математический ряд позволил относительно легко связать квадраты всех трех сторон одним правилом.Так возникла известная теорема. И египетский треугольник — это точно такая же фигура, которая подтолкнула Пифагора к самому гениальному решению. Согласно другим историческим данным, фигуре было присвоено имя греков: в то время они часто оставались в Египте, где могли заинтересоваться работой геодезистов. Существует вероятность того, что, как это часто случается с научными открытиями, обе истории произошли одновременно, поэтому невозможно с уверенностью сказать, кто первым придумал название «Египетский треугольник».Его свойства удивительны и, конечно, не исчерпываются простым соотношением размеров сторон. Его площадь и стороны представлены целыми числами. Благодаря этому применению теоремы Пифагора к нему можно получить целые числа квадратов гипотенузы и ног: 9-16-25. Конечно, это может быть простым совпадением. Но как же тогда объяснить тот факт, что египтяне считали свой «собственный» треугольник священным? Они верили в его связь со всей вселенной.

После того, как информация об этой необычной геометрической фигуре стала достоянием общественности, в мире начались поиски других подобных треугольников с целыми сторонами.Было очевидно, что они существуют

Но важность вопроса заключалась не только в математических вычислениях, но и в проверке «священных» свойств. Египтяне при всей их необычности никогда не считались глупыми — ученые до сих пор не могут объяснить, как строились пирамиды

И тут, неожиданно, обычная фигура была приписана связи с Природой и Вселенной. И действительно, самая старая найденная вавилонская клинопись содержит инструкции о подобном треугольнике со стороной, размер которой описывается 15-значным числом.В настоящее время египетский треугольник, углы которого составляют 90 (прямые), 53 и 37 градусов, находится в совершенно неожиданных местах. Например, при изучении поведения молекул обычной воды оказалось, что изменение агрегатного состояния сопровождается перестройкой пространственной конфигурации молекул, в которой можно увидеть … тот же самый египетский треугольник. Если вспомнить, что молекула воды состоит из трех атомов, то можно говорить об условных трех сторонах. Разумеется, речь не идет о полном совпадении f